Свое понимание окружающего мира человек формирует в форме высказываний (суждений, утверждений).  Высказывания могут быть выражены с помощью не только естественных языков, но и формальных.

Пример: Естественный язык - "Два умножить на два равно четыре" , формальный (математический) язык - " 2*2=4 " .

Высказывание – это форма мышления, в которой что-либо утверждается или отрицается о свойствах реальных предметов и отношениях между ними.

Высказывание может быть либо истинно, либо ложно.

Алгебра логики (высказываний) была разработана для того, чтобы можно было определять истинность или ложность составных высказываний, не вникая в их содержание.

В алгебре высказываний суждениям (простым высказываниям) ставятся в соответствие логические переменные, обозначаемые прописными буквами латинского алфавита.

Пример:

А="Два умножить на два равно четырем"

B="Два умножить на два равно пяти"

Истинному высказыванию соответствует значение логической переменной 1, а ложному - значение 0. В нашем случае первое высказывание истинно (А=1), а второе ложно (В=0).

В алгебре логики (высказываний) высказывания обозначаются именами логических переменных, которые могут принимать лишь два значения: "ИСТИНА" (1) или "ЛОЖЬ" (0).

В алгебре высказываний над высказываниями можно производить определенные логические операции, в результате которых получаются новые, составные высказывания.

Для образования новых высказываний наиболее часто используются базовые логические операции, выражаемые с помощью логических связок "и", "или", "не".

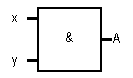
Логическое умножение (конъюнкция)

Объединение двух (или нескольких) высказываний в одно с помощью союза «и» называется операцией логического умножения или конъюнкцией.

Обозначение операции конъюнкции:  &,  ∧,  «и».

Составное высказывание, образованное в результате операции логического умножения, истинно тогда и только тогда, когда истинны все входящие в него простые высказывания.

Из переведённых ниже четырех высказываний, образованных с помощью операции логического умножения, истинно только четвертое, так как  в первых трех составных высказываниях хотя бы одно из простых высказываний ложно:

2*2=5 и 3*3=10

2*2=5 и 3*3=10

2*2=4 и 3*3=10

2*2=4 и 3*3=9

Образуем составное высказывание F, которое получится в результате конъюнкции двух простых высказываний:

F = A ∧ B

C точки зрения алгебры логики мы записали формулу функции логического умножения, аргументами которой являются логические переменные A и B, которые могут принимать значение  "истина" (1) и "ложь" (2). Сама функция логического умножения  F также может принимать лишь два значения "истина" (1) и "ложь" (2).

Таблица истинности функции логического умножения:

А	В	F = A ∧ B
0	0	0
0	1	0
1	0	0
1	1	1

Графическое представление логической операции конъюнкции:

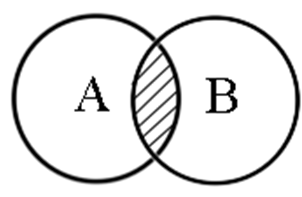
На изображении представлены два множества А и В, заштрихованная поверхность - это результат операции конъюнкции.

Логическое сложение (дизъюнкция)

Объединение двух (или нескольких) высказываний с помощью союза «или» называется операцией логического сложения или дизъюнкцией.

Обозначение операции дизъюнкции: +, ∨, «или».

Составное высказывание, образованное в результате логического сложения, истинно тогда, когда истинно хотя бы одно из входящих в него простых высказываний.

Из переведённых ниже четырех высказываний, образованных с помощью операции логического умножения, ложно только первое, так как  в последних трех составных высказываниях хотя бы одно из простых высказываний истинно:

2*2=5 или 3*3=10

2*2=5 или 3*3=10

2*2=4 или 3*3=10

2*2=4 или 3*3=9

Образуем составное высказывание F, которое получится в результате дизъюнкции двух простых высказываний:

F = A ∨ B

C точки зрения алгебры логики мы записали формулу функции логического сложения, аргументами которой являются логические переменные A и B, которые могут принимать значение  "истина" (1) и "ложь" (2). Сама функция логического сложения  F также может принимать лишь два значения "истина" (1) и "ложь" (2).

Таблица истинности функции логического сложения:

А	В	F = A ∨ B
0	0	0
0	1	1
1	0	1
1	1	1

Графическое представление логической операции дизъюнкции:

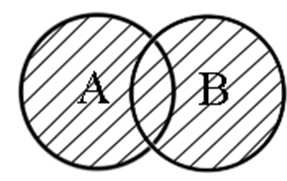
На изображении представлены два множества А и В, заштрихованная поверхность - это результат операции дизъюнкции.

Логическое отрицание (инверсия)

Присоединение частицы «не» к высказыванию называется операцией логического отрицания или инверсией.

Обозначение операции инверсия: F = ¬ A, «не».

Логическое отрицание делает истинное высказывание ложным и, наоборот, ложное – истинным.

Таблица истинности функции логического отрицания:

А	F = ¬ A
0	1
1	0

Графическое представление логической операции инверсии:

Возврат к списку уроков      Следующий урок